Continued Fractions- Pell's Equation
In we will introduce finite continued fractions. We will show that a finite continued fraction represents a rational number, and every rational number can be expressed by a finite continued fraction in a unique way. Continued fractions provide an important approach for solving Diophantine equations.
Many great mathematicians of the seventeenth and eighteenth centuries have been fascinated by continued fractions and have done work on it. Appearing in many areas of mathematics, continued fractions are interesting and useful in other areas of number theory. For instance, continued fractions are “the best” approximations of real numbers. Continued fractions, which also provide a way to learn about the decimal approximations of rational numbers, also appear in many other areas. Additionally, continued fractions provide a way to analyze solutions to Pell’s equation $x^2-Dy^2=1$. Since all integral solutions of Pell’s equation come from convergents to $\sqrt{D}$.
Finite Continued Fraction ( Rosen 1992)
An expression of the form
$a_0+\cfrac{1}{a_1 +\cfrac{1}{a_2 +\cfrac{1}{\ddots a_{n-1}+\cfrac{1}{a_n}}}}$is called as a finite continued fraction where each $a_i$ is a real number, $a_0 ≥ 0, a_{i+1} > 0$ and $i ≥ 0$. The numbers $a_1, a_2, . . . , a_n$ are the partial quotients of the finite continued fraction. The fraction is simple if each $a_i$ is an integer.
A finite continued fraction can also be written as $[a_0;a_1,a_2,\ldots,a_n]=a_0+\frac{1}{[a_1;a_2,a_3,\ldots,a_n]}=[a_0;[a_1;a_2,a_2,\ldots,a_n]]$ for $n > 0$.Note that the semicolon separates the fractional part from the integral part.
Theorem.Every finite simple continued fraction represents a rational number
Example $[2;3,4,5,6]$
This is $[2;3,4,2]$
THEOREM : Every rational number is uniquely represented by a finite continued fraction.
Example: represent $\frac{225}{157}$
Suppose $a_n > 1$ in the finite simple continued fraction $[a_0; a_1, . . . , a_n]$. Since $a_n = (a_{n} − 1) + \frac{1}{1}$ , it follows that $[a_0; a_1, . . . , a_n] = [a_0; a1, . . . , a_{n} − 1, 1]$.
For example,
$[1; 2, 3, 4, 5] = [1; 2, 3, 4, 1]$.
On the other hand, let $a_n = 1$. Then $[a_0; a_1, . . . , a_n] = [a_0; a_1, . . . , a_{n−1}, 1] = [a_0, a_1, . . . , a_{n−1} +1]$
For example, $[1; 2, 3, 4, 1] = [1; 2, 3, 5]$.Thus, every rational number can be written as a finite simple continued fraction in two different ways. In other words, the continued fraction representation of a rational number is not unique.
Example:
In the example 2.4 $\frac{67}{29}$ is represented as $[2;3,4,2]$
Since $2=1+1$, it can be written
Therefore, it can also be denoted as $[2;3, 4,1,1]$
An infinite continued fraction is an expression of the form
$a_0+\cfrac{1}{a_1 +\cfrac{1}{a_2 +\cfrac{1}{\ddots }}}$
where $a_0,a_1,\ldots$ are real numbers with $a_1,a_2,\ldots,a_n$ are positive with $a_0 \ge 0$ and it is denoted by $[a_0,a_1,\ldots,a_n,\ldots]$.If the real numbers $a_0,a_1,\ldots,a_n$ are all integers,
then the continued fraction is called simple.
Example:
THEOREM : The infinite simple continued fraction $[a_0; a_1, a_2, . . .]$ represents an irrational number.
Example:the continued fraction expansion of
is:
Convergents of a Continued Fraction
By truncating the continued fraction for $x = [a_0; a_1, . . . , a_n]$ at the various plus signs , we can generate a sequence $\{c_k\}$ of approximations of $x$, where $0 ≤ k ≤ n$; thus, $ck = [a_0, a_1, \ldots, a_k];$ $c_k$ is called the $k$th convergent of $x$, a concept introduced by Wallis in his Opera Mathematica.
Theorem:The $k$th convergent of the finite simple continued fraction $[a_0; a_1, \ldots , a_n]$ is $$c_k = \frac{p_k}{q_k}$$
where $2 ≤ k ≤ n$, and the sequences $\{pk\}$ and $\{qk\}$ are defined recursively as follows:
Example:
THEOREM Let $c_k = \frac{p_k}{q_k}$ be the $k$th convergent of the simple continued fraction $[a_0; a_1, . . . , a_n]$, where $1 ≤ k ≤ n$. Then $$p_kq_{k−1} −q_kp_{k−1} = (−1)^{k−1}.$$
Continued Fractions and LDEs
Recall that the LDE $ax + by = c$ is solvable if and only if $d | c$,where $d = (a, b)$. If $x_0, y_0$ is a particular solution, then it has infinitely many solutions $x = x_0 +(b/d)t, y = y_0 −(a/d)t.$
Continued fractions can be employed to solve LDEs. To see this, first consider the LDE $ax+by = 1$, where $b >$ 0 and $gcd(a, b) = 1$. Since $a/b$ is a rational number, it can be represented by a continued fraction $[a_0; a_1, . . . , a_n]$. Then $$c_n = \frac{p_n}{q_n}=\frac{a}{b}$$
Since $(p_n, q_n) = 1 = (a, b)$, it follows that $a = p_n$ and $b = q_n$.
By Theorem , $p_nq_{n−1} − q_np_{n−1} = (−1)^{n−1}$; so $aq_{n−1} − bp_{n−1} = (−1)^{n−1}$.
When $n$ is odd, it becomes $aq_{n−1} + b(−p_{n−1}) = 1$; so $x_0 = q_{n−1}, y_0 =−p_{n−1}$ is a solution of the LDE $ax + by = 1$. On the other hand, when $n$ is even, it becomes $a(−q_{n−1})+bp_{n−1} = 1$; so $x_0 =−q_{n−1}, y_0 = p_{n−1}$ is a solution.
When $x_0, y_0$ is a solution of the LDE $ax + by = $1, $ax_0 + by_0 = 1$; so $a(cx_0) +b(cy_0) = c$; thus, $cx_0, cy_0$ is a particular solution of the LDE $ax + by = c$.
The following example illustrates this technique.
By Theorem , $p_3q_2 − q_3p_2 = (−1)^{3−1}$; that is, $(−63) · 4 + 23 · 11 = 1$.Consequently, $x_0 = 4, y_0 = 11$ is a particular solution of the LDE $(−63)x+23y = 1.$Therefore, $7x_0 = 28, 7y_0 = 77 is a particular solution of the LDE (−63)x+23y = 7.$So, by Theorem, its general solution is $x = 7x_0 +bt = 28+23t, y = 7y_0 −at =77+63t.$
Pell's Equation
The integer 10 has an intriguing property: One less than the number is a square: $10−1 = 3^2$; and one less than one-half of the number is also a square: $10/2−1 = 2^2$. The next number that has the same property is $290: 290−1 = 17^2$ and $290/2−1 = 12^2$.
Are there are other such numbers? If yes, how do we find them?
To discover this, let $r$ be such a number. Then $r − 1 = x^2$ and $r/2 − 1 = y^2$,for some positive integers $x$ and $y$. Eliminating $r$ between the equations yields the Diophantine equation $$x^2 −2y^2 = 1$$.
Clearly x = 3, y = 2 is a solution of the equation:
$3^2 −2.2^2 = 1$. Likewise, $x = 17, y = 12$ is also a solution: $17^2 − 2 · 12^2 = 1$.
More generally, we would like to solve the nonlinear diophantine equation $$x^2 − Ny^2 = 1$$. This equation is commonly called Pell’s equation, after John Pell.
Trivial Solutions
When $N = 0$, we halve $x = \pm 1$, but $y$ is arbitrary. They are trivial solutions. If $N ≤−2, x^2 − Ny^2 ≥ 0$; so the only solutions are the trivial ones with $y = 0$, namely, $x=±1, y = 0$. If $N =−1$, then $x^2 + y^2 = 1$; again, the only solutions are the trivial ones, namely, $(±1, 0), (0,±1)$.
Nontrivial Solutions
So we assume that $N > 0$. If $N$ is a square $m^2$, then Pell’s equation yields $1 = x^2 −m^2y^2 = (x −my)(x +my)$.Then $x − my = 1 = x + my$ or $x − my = −1 = x + my$. Solving these two linear systems, we get a solution in each case.Thus, when $N < 0$ or $N$ is a square, we know the exact solutions, and they are finite in number. So we turn to the case when $N$ is positive and square-free.
The simplest such Pell equation is when $N = 2: x^2 − 2y^2 = 1$. Because $3^2 − 2.2^2 = 1, x = 3, y = 2$ is a solution; so is $x = 17, y = 12$. Thus, $x^2−2y^2 = 1$ has at least two solutions. In fact, we shall see later that it has infinitely many solutions.
- If $x, y$ is a solution, then so are $x,−y$; and $−x,±y$. Thus, the nontrivial solutions occur in quadruples. So we can always assume that $x$ and $y$ are positive.
- Because $1+Ny^2 = x^2$, nontrivial solutions can be found by computing $1+Ny^2$ and then determining if it is a square. For example, $1 + 92 · 120^2 = 1151^2$;so $x = 1151, y = 120$ is a solution of $x^2 − 92y^2 = 1$, as noted earlier. This method, although it sounds simple in theory, is not practical.
- Let $a, b$ be a solution. Then $a^2 − Nb^2 = (a + b\sqrt{N})(a − b\sqrt{N})$, so numbers of the form $a+b \sqrt{N}$ play an important role in finding the solutions. For convenience, we then say that the irrational number $a + b \sqrt{N}$ yields a solution.
LEMMA : If $r$ and $s$ yield solutions of Pell’s equation $x^2 −Ny^2 = 1$, where $N > 0$ and is squarefree, then so does $rs$.
Example:Let $r = 3 + 2\sqrt{2}$ and $s = 17 + 12\sqrt{2}$ yield two solutions of $x^2 − 2y^2 = 1$. Find two additional solutions.
Solution
By Lemma $rs = (3 · 17+2 · 12 · 2)+(3 · 12+2 · 17)\sqrt{2} = 99+70\sqrt{2}$ yields a solution:
$99^2 − 2 · 70^2 = 1$. Likewise,$r^2 = (3 · 3 + 2 · 2 · 2) + (3 · 2 + 2 · 3)\sqrt{2} =17+12\sqrt{2}$ also yields a solution
The following lemma helps us determine the least solution of $x^2 − Ny^2 = 1$,where $N > 0$ and is square-free.
LEMMA Let $N > 0$ and square-free. Suppose $r = a + b\sqrt{N}$ and $s = c + d\sqrt{N}$ yield solutions of $x^2 −Ny^2 = 1$, where $a, b, c, d > 0$. Then $r < s$ if and only if $a < c$.
THEOREM: Suppose $α + β\sqrt{N}$ yields the least solution of $x^2 − Ny^2 = 1$, where $N > 0$ and is square-free. Then the equation has infinitely many solutions, given by
$$x=[ (\alpha + \beta \sqrt{N})^n + (\alpha - \beta \sqrt{N})^n]/2$$
$$y=[ (\alpha + \beta \sqrt{N})^n - (\alpha - \beta \sqrt{N})^n]/(2\sqrt{N})$$
Example:Using the fact that $3 + 2\sqrt{2}$ yields the least solution of $x^2 − 2y^2 = 1$, find two new solutions.
By the above theorem
$$x=[ (3 + 2\sqrt{2})^n + (3 -2 \sqrt{2})^n]/2$$
$$y=[ (3 + 2 \sqrt{2})^n - (3 - 2 \sqrt{2})^n]/(2\sqrt{2})$$
is a solution for every integer $n$. Notice that $n = 1$ yields the least solution.
When $n = 2$,
$$x=[ (3 + 2\sqrt{2})^2 + (3 -2 \sqrt{2})^2]/2=17$$
and
$$y=[ (3 + 2 \sqrt{2})^2- (3 - 2 \sqrt{2})^2]/(2\sqrt{2})=12$$
When $n = 3$,
$$x=[ (3 + 2\sqrt{2})^3 + (3 -2 \sqrt{2})^3]/2=99$$
and
$$y=[ (3 + 2 \sqrt{2})^3- (3 - 2 \sqrt{2})^3]/(2\sqrt{2})=70$$
Thus $17+12 \sqrt{2}$ and $99=70\sqrt{2}$ yield two new solutions.




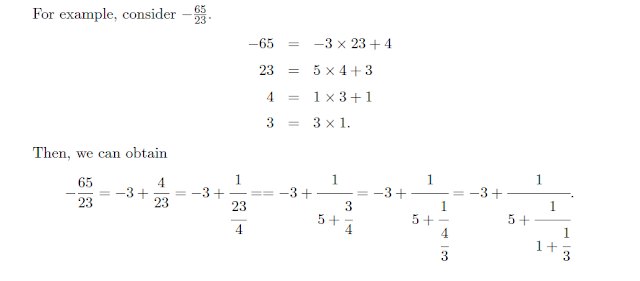







Comments
Post a Comment